| c语言, Linux,

用python设计高通（HPF）和低通（LPF）数字滤波器

在数学工具中，做滤波器的设计很简单，用起来也很简单，但是要在嵌入式设备中使用滤波器，必须能用c语言写，没有现成的库可以用，一般都是自己写。

数字滤波一般分为时域滤波和频域滤波，在这里我们设计时域滤波器。时域滤波器分为无限脉冲响应IIR和有限脉冲响应FIR两种。IIR滤波器的优点是可以用较低的阶数（相比同样指标的FIR滤波器）实现滤波器。缺点一：不是线性相位，只能用于对相位信息不敏感的信号(如音频信号）。缺点二：有可能是不稳定的，也可能由于量化舍入等因素引起的误差最终导致IIR滤波器不稳定。FIR滤波器的优点是可以设计成具有线性相位的，并且是稳定的，缺点是阶数高，也就是说计算量大。

嵌入式系统一般都是希望节省计算量，所以没的选了，IIR吧。

一、设计高通数字滤波器

使用python设计，推荐使用jupyter-notebook，可以方便显示曲线，方便调试。本文已bufferworth滤波器为例。

以下代码为高通滤波器的设计代码（python）

from scipy.signal import butter, freqz
import matplotlib.pyplot as plt
from math import pi
import numpy as np

f_s = 100 # Sample frequency in Hz
f_c = 1 # Cut-off frequency in Hz
order = 3 # Order of the butterworth filter

omega_c = 2 * pi * f_c # Cut-off angular frequency
omega_c_d = omega_c / f_s # Normalized cut-off frequency (digital)

# Design the digital Butterworth filter
b, a = butter(order, omega_c_d / pi, 'highpass')
print('Coefficients')
print("b =", b) # Print the coefficients
print("a =", a)

w, H = freqz(b, a, 4096) # Calculate the frequency response
w *= f_s / (2 * pi) # Convert from rad/sample to Hz

# Plot the amplitude response
plt.subplot(2, 1, 1)
plt.suptitle('Bode Plot')
H_dB = 20 * np.log10(abs(H)) # Convert modulus of H to dB
plt.plot(w, H_dB)
plt.ylabel('Magnitude [dB]')
plt.xlim(0, f_s / 2)
plt.ylim(-80, 6)
plt.axvline(f_c, color='red')
plt.axhline(-3, linewidth=0.8, color='black', linestyle=':')

# Plot the phase response
plt.subplot(2, 1, 2)
phi = np.angle(H) # Argument of H
phi = np.unwrap(phi) # Remove discontinuities
phi *= 180 / pi # and convert to degrees
plt.plot(w, phi)
plt.xlabel('Frequency [Hz]')
plt.ylabel('Phase [°]')
plt.xlim(0, f_s / 2)
plt.ylim(-360, 0)
plt.yticks([-360, -270, -180, -90, 0])
plt.axvline(f_c, color='red')

plt.show()

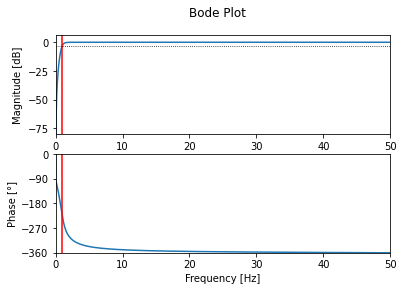
上面的代码，设计了一个采样频率100Hz，截止频率1Hz的高通滤波器。结果如下：

Coefficients
b = [ 0.93909165 -2.81727496  2.81727496 -0.93909165]
a = [ 1.         -2.87435689  2.7564832  -0.88189313]

滤波器的伯德图如下：

二、设计低通滤波器

与高通滤波器类似，python代码如下：

from scipy.signal import butter, freqz
import matplotlib.pyplot as plt
from math import pi
import numpy as np

f_s = 100 # Sample frequency in Hz
f_c = 5 # Cut-off frequency in Hz
order = 3 # Order of the butterworth filter

omega_c = 2 * pi * f_c # Cut-off angular frequency
omega_c_d = omega_c / f_s # Normalized cut-off frequency (digital)

# Design the digital Butterworth filter
b, a = butter(order, omega_c_d / pi)
print('Coefficients')
print("b =", b) # Print the coefficients
print("a =", a)

w, H = freqz(b, a, 4096) # Calculate the frequency response
w *= f_s / (2 * pi) # Convert from rad/sample to Hz

# Plot the amplitude response
plt.subplot(2, 1, 1)
plt.suptitle('Bode Plot')
H_dB = 20 * np.log10(abs(H)) # Convert modulus of H to dB
plt.plot(w, H_dB)
plt.ylabel('Magnitude [dB]')
plt.xlim(0, f_s / 2)
plt.ylim(-80, 6)
plt.axvline(f_c, color='red')
plt.axhline(-3, linewidth=0.8, color='black', linestyle=':')

# Plot the phase response
plt.subplot(2, 1, 2)
phi = np.angle(H) # Argument of H
phi = np.unwrap(phi) # Remove discontinuities
phi *= 180 / pi # and convert to degrees
plt.plot(w, phi)
plt.xlabel('Frequency [Hz]')
plt.ylabel('Phase [°]')
plt.xlim(0, f_s / 2)
plt.ylim(-360, 0)
plt.yticks([-360, -270, -180, -90, 0])
plt.axvline(f_c, color='red')

plt.show()

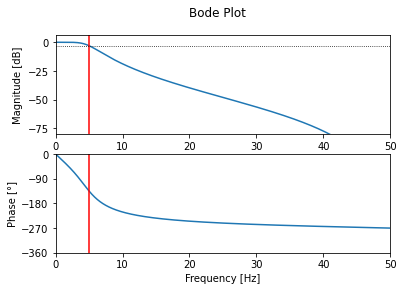
设计结果：

Coefficients
b = [0.00289819 0.00869458 0.00869458 0.00289819]
a = [ 1.         -2.37409474  1.92935567 -0.53207537]

伯德图：

三、如何写C代码

有了滤波器的a和b向量，就可以使用了。

IIR数字滤波器的一般形式：

y(n) = SUM(b[m]*x[m]) - SUM(a[n]*y[n])

其中，m从0到滤波器的阶数ORDER，n从1到ORDER。

具体代码如下：

低通滤波器

// cutoff 1Hz
void sensor_hpf(led_data_t * sen)
{
float x, y;
int i;
const float b[HPF_ORDER + 1] = {0.93909165, -2.81727496, 2.81727496, -0.93909165};
const float a[HPF_ORDER + 1] = {1.0, -2.87435689, 2.7564832, -0.88189313};

for (i=HPF_ORDER;i>0;i--){
sen->hx[i] = sen->hx[i - 1];
sen->hy[i] = sen->hy[i - 1];
}
sen->hx[0] = sen->filtered;

//y(i)=b1*x(i)+b2*x(i-1)+b3*x(i-2)+b4*x(i-3)-a2*y(i-1)-a3*y(i-2)-a4*y(i-3);
x = 0;
y = 0;
for (i=0;i<=HPF_ORDER;i++){
x += b[i] * sen->hx[i];
}
for (i=1;i<=HPF_ORDER;i++){
y += a[i] * sen->hy[i];
}
sen->hy[0] = x - y;
sen->hpfed = (int16_t)sen->hy[0];
}

高通滤波器

// cutoff 5Hz
void sensor_lpf(led_data_t * sen)
{
float x, y;
int i;
const float b[LPF_ORDER + 1] = {0.00289819, 0.00869458, 0.00869458, 0.00289819};
const float a[LPF_ORDER + 1] = { 1.0, -2.37409474, 1.92935567, -0.53207537};

for (i=LPF_ORDER;i>0;i--){
sen->x[i] = sen->x[i - 1];
sen->y[i] = sen->y[i - 1];
}
sen->x[0] = sen->raw;

//y(i)=b1*x(i)+b2*x(i-1)+b3*x(i-2)+b4*x(i-3)-a2*y(i-1)-a3*y(i-2)-a4*y(i-3);
x = 0;
y = 0;
for (i=0;i<=LPF_ORDER;i++){
x += b[i] * sen->x[i];
}
for (i=1;i<=LPF_ORDER;i++){
y += a[i] * sen->y[i];
}
sen->y[0] = x - y;
sen->filtered = (uint16_t)sen->y[0];
}

 

 

 

 

欢迎转载，本文地址: https://blog.prodrich.com/detail/62/

带着使命来到世上的你，给他人提供价值，才有价值